Kurs: Der menschengemachte Klimawandel: Ursachen, Effekte und Lösungswege

Finanzwirtschaftliche Entscheidungskalküle mit Berücksichtigung des Klimaschutzes

Integration nicht-monetärer Ziele

Die theoretische Grundlage für die Auswahl von Portfolios mit Berücksichtigung von nicht-monetären Zielen kann durch die Erweiterung unserer bisherigen Nutzenfunktion erfolgen zu:

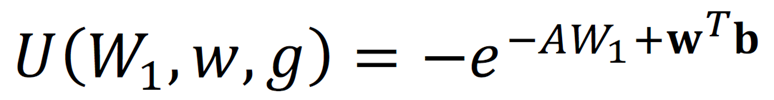
Diese Nutzenfunktion stellt eine multikriterielle Nutzenfunktion, konkret eine bikriterielle Nutzenfunktion. Dabei wird die Annahme der Nutzenadditivität getroffen, nach der die Nutzwerte der Assets miteinander addieren können. Der Nx1 Vektor 𝐛 beinhaltet die persönlich empfundene, nicht-monetäre Nutzwerte von jedem risikobehafteten Asset. Das risikolose Asset stiftet uns keinen nicht-monetäre Nutzen. Der Vektor der Nutzwerte enthält eine individuelle und eine unternehmensspezifische Komponente:

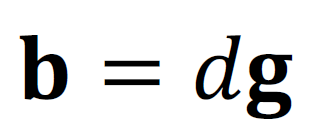
wobei 𝐠 ein Nx1 Vektor von unternehmensspezifische, nicht-monetären Charakteristiken und 𝑑 ≥ 0 ein Skalar ist, der unsere Vorliebe für diese nicht- monetäre Charakteristiken anzeigt. Als nicht-monetäre Charakteristiken könnten wir beispielsweise CO₂-Ausstoß, CO₂-Einsparung, Beitrag zur Erreichung von „Sustainable Development Goals“ (SDG) der UN oder andere Kennzahlen heranziehen, die dem Klimaschutz dienen.

Um die formalen Ableitungen einfach zu halten, nehmen wir auch an, dass alle Personen die wahren Werten von 𝐠 kennen. Folglich gibt es keine Unsicherheit über die unternehmensspezifische, nicht-monetären Charakteristiken. Unsicherheiten existieren nur über die zukünftige unternehmensspezifische Rendite. Für den Rest der Lektion nehmen wir einfachheitshalber an, dass diese Charakteristik anzeigt, wie „grün“ ein Asset ist. Positive Werte dieser Charakteristik zeigen grüne Assets an, negative Werte „braune“ Assets. Je höher die Charakteristik, desto grüner ist das Asset und desto mehr wird dieses Asset zum Klimaschutz-Ziel beitragen. Diese Konkretisierung erleichtert uns die Interpretationen durch ein konkretes Beispiel. Der Vektor 𝐛 zeigt also an, wie viel Nutzen uns durch das Halten von N Assets gestiftet wird. Je höher 𝑑 ist, desto mehr Nutzen stiftet uns ein grünes Asset und desto höher ist folglich unsere Vorliebe für grüne Assets.

In analogen Schritten zur letzten Lektion können wir die optimalen Portfolioanteilsgewichte für Personen ableiten, die Vorlieben für grüne Assets haben:

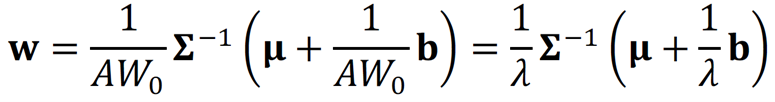
Das Anteilsgewicht eines Assets in unserem Portfolio wird umso höher sein, je geringer sein Risikobeitrag zum Portfolio (angezeigt durch höhere Werte von 𝚺-1), je höher seine Rendite (𝛍), je höher unsere Vorliebe für grüne Assets (𝑑) und je höher unternehmensspezifische Charakteristika des Grünseins (𝐠) sind. Die Gleichung für optimale Anteilsgewichte abstrahiert einfachheitshalber von der Budget- und anderen Restriktionen. Wenn wir keine Vorlieben für grüne Assets haben (𝑑 = 0), dann werden wir exakt das gleiche Portfolio halten, wie eine Person, die nicht- monetäre Ziele gar nicht berücksichtigt (vgl. Lektion 2). Wenn wir eine Vorliebe für grüne Assets haben (𝑑 > 0), dann werden in unserem Portfolio Assets mit 𝑔_i > 0 (𝑔_i < 0) in unserem Portfolio eine höhere (geringere) Gewichtung im Vergleich zu Personen ohne nicht-monetäre Ziele aufweisen.

Grüne Assets und Marktpreise

Die interessante Frage an dieser Stelle ist, wie sich unsere Vorliebe für grüne Assets auf die Marktpreise auswirkt. Dazu müssen im Markt mindestens einige Personen existieren, die eine Vorliebe für nicht-monetäre Ziele aufweisen. Unser entscheidungstheoretisches Grundmodell mit zusätzlichen Annahmen hilft uns hier weiter. Dazu nehmen wir hier an, dass die Risikoaversion aller Marktteilnehmenden identisch ist, also 𝜆_j= 𝜆 für jede Person 𝑗. Wir definieren ferner

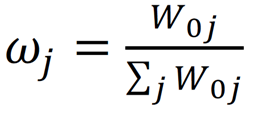
als den Anteil des Vermögens der Person j am Gesamtvermögen eines Marktes. Für die Gewichte des Marktportfolios w_m muss dann gelten:

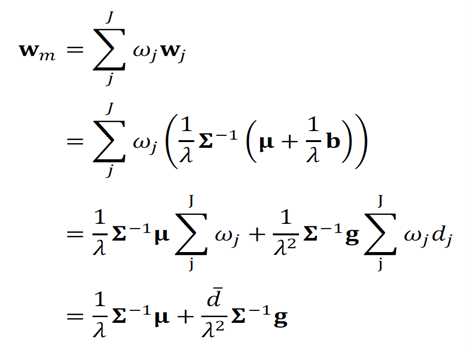
wobei

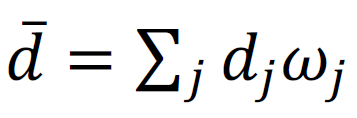
der vermögensgewichtete Durchschnitt der Vorlieben für grüne Assets ist und

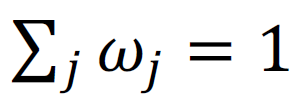
Die Gleichung für die Gewichte des Marktportfolios können wir nach den erwarteten Renditen der Assets auflösen und erhalten:

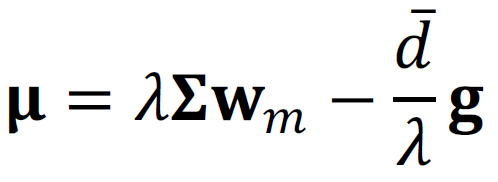
Die erwarte Rendite des Marktes, die sogenannte Marktrisikoprämie, erhalten wir durch die Multiplikation mit den Anteilsgewichten des Marktportfolios:

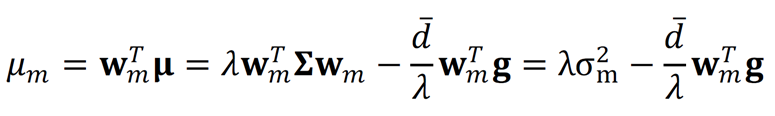
Zur Vereinfachung nehmen wir für die Marktrisikoprämie

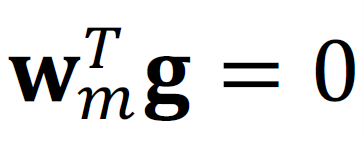
an. Damit nehmen wir an, dass die Marktrisikoprämie unabhängig von unseren Vorlieben für grüne Assets ist. Daraus ergibt sich

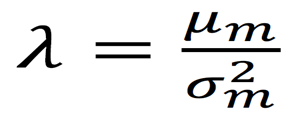
Wenn wir 𝜆 in die Gleichung für die erwarteten Renditen der Assets einsetzen, erhalten wir:

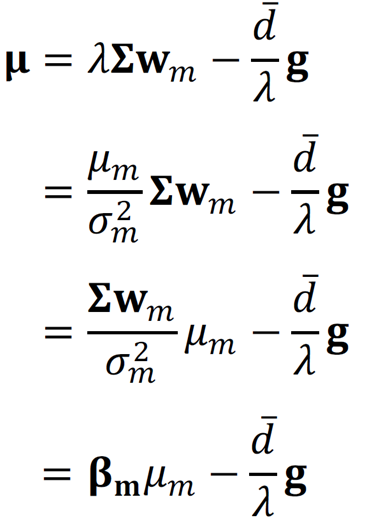
Die erwartete Rendite 𝐸(𝑟_i) für das Asset 𝑖 ist somit:

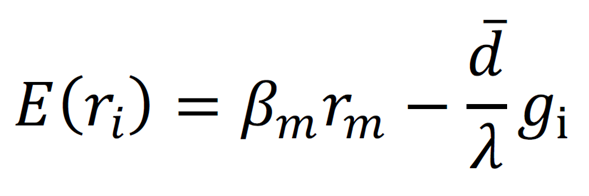
Wir beobachten also eine Abweichung der erwarteten Asset-Rendite im Marktgleichgewicht im Vergleich zur erwarteten CAPM-Rendite wegen der Berücksichtigung von nicht-monetären Zielen. Solange die Anzahl der Personen, denen Nachhaltigkeit wichtig ist, nicht Null ist, ist

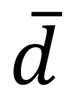
positiv und die erwarteten Renditen von Assets sinken mit steigenden Werten von 𝐠. Je grüner also ein Asset ist, desto geringer wird seine Rendite im Marktgleichgewicht sein.

Angesichts ihrer Vorliebe für grüne Assets sind manche Personen bereit, mehr für umweltfreundlichere Unternehmen im Vergleich zum CAPM zu zahlen, wodurch die erwarteten Renditen der grünen Assets sinken. Dieses Ergebnis mag auf den ersten Blick widersinnig erscheinen, denn entgegen der populären Meinung legt es nahe, dass die grünen Assets schlechter als der Markt und schlechter als braune Assets performen. Dieses Ergebnis ist aber konsistent, weil unser persönlicher Nutzen nicht nur durch monetäre Ziele, sondern auch durch nicht-monetäre Ziele (z.B. Klimaschutz) gesteigert wird. Vereinfachend gesagt:

Unser Nutzen ist gleichgeblieben, aber es gibt jetzt zwei Komponenten (Vermögen und Klimaschutz), die uns Nutzen stiften.

Aus der Sicht der grünen Unternehmen ist das Ergebnis ebenfalls positiv, weil diese Unternehmen geringere Kapitalkosten und somit geringere Finanzierungskosten zahlen müssen, solange sie grüne Projekte umsetzen.

Die Anteilsgewichte von Portfolios für Personen mit Vorliebe für grüne Assets können wir weiter vereinfachen. Dazu setzen wir die erwarteten Assetrenditen 𝛍 in die Gleichung für optimale Anteilsgewichte ein und erhalten:

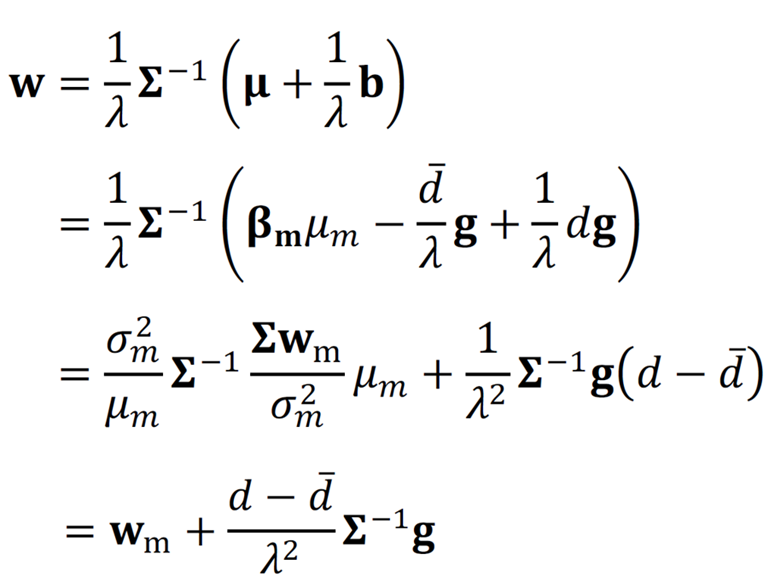
Die letzte Gleichung impliziert ein vereinfachtes 3-Fonds-Seperationstheorem, da wir mit Überschussrenditen arbeiten.

Demnach kann jedes Portfolio mit drei Assets nachgebildet werden:

dem risikofreien Asset,
dem Marktportfolio und
einem Portfolio grüner Assets („ESG-Portfolio“).

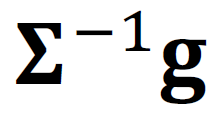
Die Anteilsgewichte für das ESG-Portfolio sind ein Vielfaches von

Wir haben bisher betont, dass zumindest einige Personen eine Vorliebe für grüne Assets (𝑑 > 0) haben müssen, weil ansonsten niemand in das ESG-Portfolio

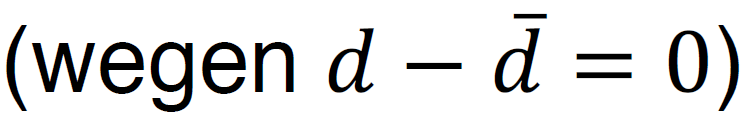
investiert. Interessanterweise wird auch dann niemand in das ESG-Portfolio investieren, wenn alle Personen identische Vorlieben

aufweisen. Unterschiedliche Vorlieben für grüne Assets ist also eine Grundvoraussetzung, dass überhaupt in das ESG- Portfolio investiert wird. Die Personen, die eine durchschnittliche Vorliebe für grüne Assets

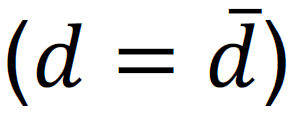
haben, werden ausschließlich das Marktportfolio halten. Personen, die keine Vorliebe für grüne Assets haben (𝑑 = 0), müssen mehr in braune Assets investieren als es sie im Marktportfolio gibt. D.h. eine Person ohne Vorliebe für grüne Assets kann nicht nur das Marktportfolio halten, sondern muss zusätzliche umweltunfreundliche Assets kaufen.

Wir können sogar angeben, wie viel wir in das risikofreie Asset, das Marktportfolio und in das ESG-Portfolio investieren sollen. Die Anteile hängen selbstverständlich von der individuellen Risikoaversion sowie von der individuellen Vorliebe für grüne Assets ab. In das risikolose Asset sollen wir einen Anteil unseres Vermögens 𝑤_f investieren (oder uns verschulden), den wir weder in das Marktportfolio noch in das ESG-Portfolio investieren. Den relativen Anteil bestimmen wir mit:

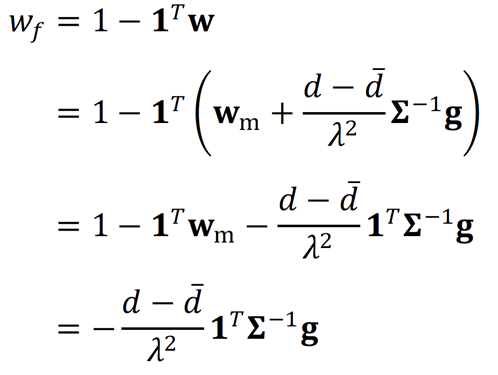
Wir investieren in ein risikoloses Asset, wenn 𝑤_f > 0 und verschulden uns, wenn 𝑤_f < 0.

Den restlichen Geldbetrag investieren wir in Aktien, wobei wir einen Anteil ϕ in grüne Aktien und (1 − 𝜙) in das Marktportfolio investieren. Damit wir eine Standardisierung der Gewichte 𝐰 auf 1 bekommen, multiplizieren wir die Gleichung mit optimalen Anteilsgewichten mit

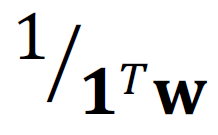
und erhalten:

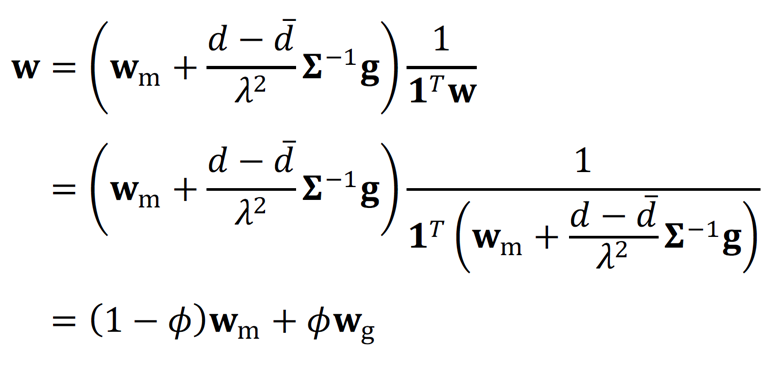
mit

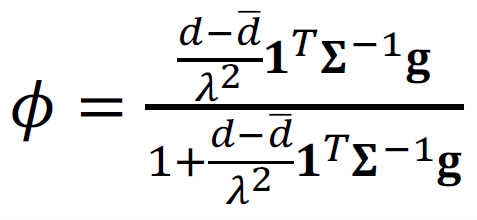
und

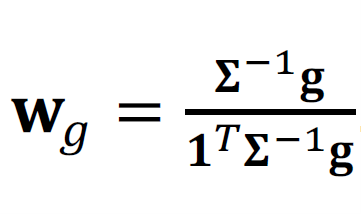
Personen mit einer überdurchschnittlichen Vorliebe für grüne Assets

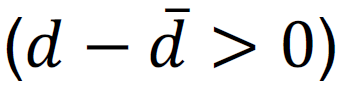
werden weniger in das Marktportfolio und mehr (weniger) in das ESG-Portfolio investieren, wenn das Grünsein des Portfolios positiv (negativ) ist, d.h.

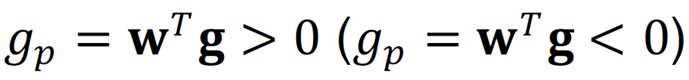
Die vorliegende Lektion hat das finanztheoretische Grundmodell skizziert, wenn Personen zusätzlich zu monetären Zielen auch nicht-monetäre Ziele verfolgen. Daraus haben sich Implikationen für die Renditen von grünen und braunen Assets ergeben, denn durch die Zusatznachfrage nach grünen Assets sinken ihre erwarteten Renditen, wenn zumindest einige Personen eine Vorliebe für grüne Assets haben (𝑑_j > 0).

Weiterführende Fragen

Wenn Sie sich noch einmal tiefergehender mit den Inhalten dieser Lektion beschäftigen möchten, beantworten Sie für sich die folgenden Fragen:

In der Lektion wird ausgehend von der erweiterten Erwartungsnutzenfunktion und normalverteilten Renditen die Formel zur Berechnung der optimalen Gewichte 𝐰 ohne die Zwischenschritte dargestellt. Lösen Sie selbst nach 𝐰 auf und zeigen Sie alle Zwischenschritte.
Die Gleichung für die optimalen Gewichte ignoriert die sogenannte Budget- Restriktion 𝐰^T 𝟏 = 1 mit 𝟏 als Nx1 Einsen-Vektor, nach der wir nicht mehr Kapital als uns zur Verfügung steht, ausgeben dürfen. Wir haben bisher angenommen, dass wir fehlendes Geld als Kredit aufnehmen können oder falls Geld übrig ist, dieses in das risikolose Asset investieren. Leiten Sie die Formel für die optimalen Gewichte mit Berücksichtigung der Budget- Restriktion ab. Hinweis: Nutzen Sie die Lagrange-Funktion in der Optimierung.
Nehmen wir drei Assets an, deren erwartete Renditen 5%, 7% und 10% sind. Die Kovarianzmarix ist

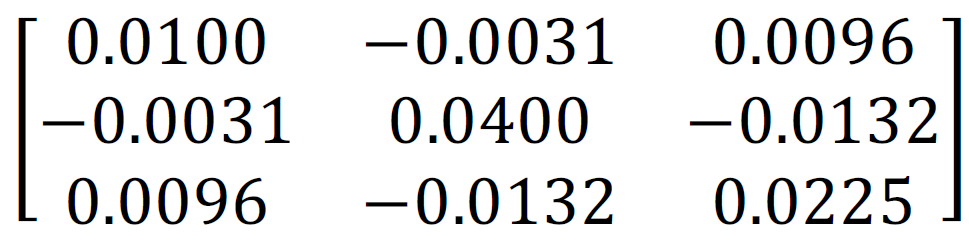
Die ESG-Werte sind 5, 3, -5. Was ist die jeweilige optimale Kapitalaufteilung für Personen mit einer absoluten Risikoaversion von 11, einem Vermögen von 1 und einer Vorliebe für grüne Assets von 3, 4 und 5?
Benutzen Sie die Angaben aus der Aufgabe 3. und bestimmen Sie die Anteilsgewichte des Marktportfolios.
Benutzen Sie die Angaben aus der Aufgabe 3. und bestimmen Sie die Anteilsgewichte des ESG-Portfolios.
Benutzen Sie die Angaben aus der Aufgabe 3. und bestimmen Sie, wie viel Vermögen sollen die Personen in die risikofreie Anlage, in das Marktportfolio und in das ESG-Portfolio investieren?

Zugrundeliegende und weiterführende Literaturhinweise

Die theoretischen Grundlagen für diese Lektion bieten die Einführungen von:

Pedersen, L. H., Fitzgibbons, S., & Pomorski, L. (2021). Responsible investing: The ESG-efficient frontier. Journal of Financial Economics, 142(2), 572-597.
Stroebel, J., & Wurgler, J. (2021). What do you think about climate finance?. Journal of Financial Economics, 142(2), 487-498.
Flammer, C. (2021). Corporate green bonds. Journal of Financial Economics, 142(2), 499-516.
Bolton, P., & Kacperczyk, M. (2021). Do investors care about carbon risk?. Journal of financial economics, 142(2), 517-549.
Pástor, Ľ., Stambaugh, R. F., & Taylor, L. A. (2021). Sustainable investing in equilibrium. Journal of Financial Economics, 142(2), 550-571.
Schlenker, W., & Taylor, C. A. (2021). Market expectations of a warming climate. Journal of Financial Economics, 142(2), 627-640.
Azar, J., Duro, M., Kadach, I., & Ormazabal, G. (2021). The big three and corporate carbon emissions around the world. Journal of Financial Economics, 142(2), 674-696.
Heeb, F., Kölbel, J.F., Paetzold, F., Zeisberger. S. (2022). Do Investors Care about Impact?, The Review of Financial Studies.

Der menschengemachte Klimawandel: Ursachen, Effekte und Lösungswege